Derivative Of Arctan
Find the Derivative - d/dx y=arctan(1/x) Differentiate using the chain rule, which states that is where. Tap for more steps. To apply the Chain Rule, set as. D/dx arctan(1/x) = -1/(x^2+1) We seek: d/dx arctan(1/x) Using the standard result: d/dx tanx=1/(1+x^2) In conjunction with the power rule and the chain rule we get: d/dx arctan(1/x) = 1/(1+(1/x)^2) d/dx (1/x) ' ' = 1/(1+1/x^2) (-1/x^2) ' ' = -1/((1+1/x^2)x^2) ' ' = -1/(x^2+1) Observation: The astute reader will notice that: d/dx arctan(1/x) = -d/dx arctan x From which we conclude that.
Derivative Of Tangent – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. Common trigonometric functions include sin(x), cos(x) and tan(x). For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a). f ′(a) is the rate of change of sin(x) at a particular point.
All derivatives of circular trigonometric functions can be found using those of sin(x) and cos(x). The quotient rule is then implemented to differentiate the resulting expression. Finding the derivatives of the inverse trigonometric functions involves using implicit differentiation and the derivatives of regular trigonometric functions.
Derivative Of Tangent
To find the derivative of a tangent of x, we’ll start by writing tan x as sin x/cos x and then use the quotient rule to differentiate.
The quotient rule says that if two functions are differentiable, then the quotient is also differentiable. Here’s the quotient rule applied to tan x when in form of sin x/cos x
Now we know that the derivative of sin x is cos x and the derivative of cos x is -sin x. Substituting these derivatives in the parentheses and simplifying, we get
Now there are two trigonometric identities we can use to simplify this problem
- sin²x + cos²x = 1
- sec x = 1/cos x
And that’s it, we are done! The derivative of tan x is sec²x.
However, there may be more to finding derivatives of the tangent. In the general case, tan x is the tangent of a function of x, such as tang(x). Note in the simple case, g(x) = x.

Generally, we are looking for
Derivative Of Inverse Tangent
The following are the formulas for the derivatives of the inverse trigonometric functions
We let y=arctan x
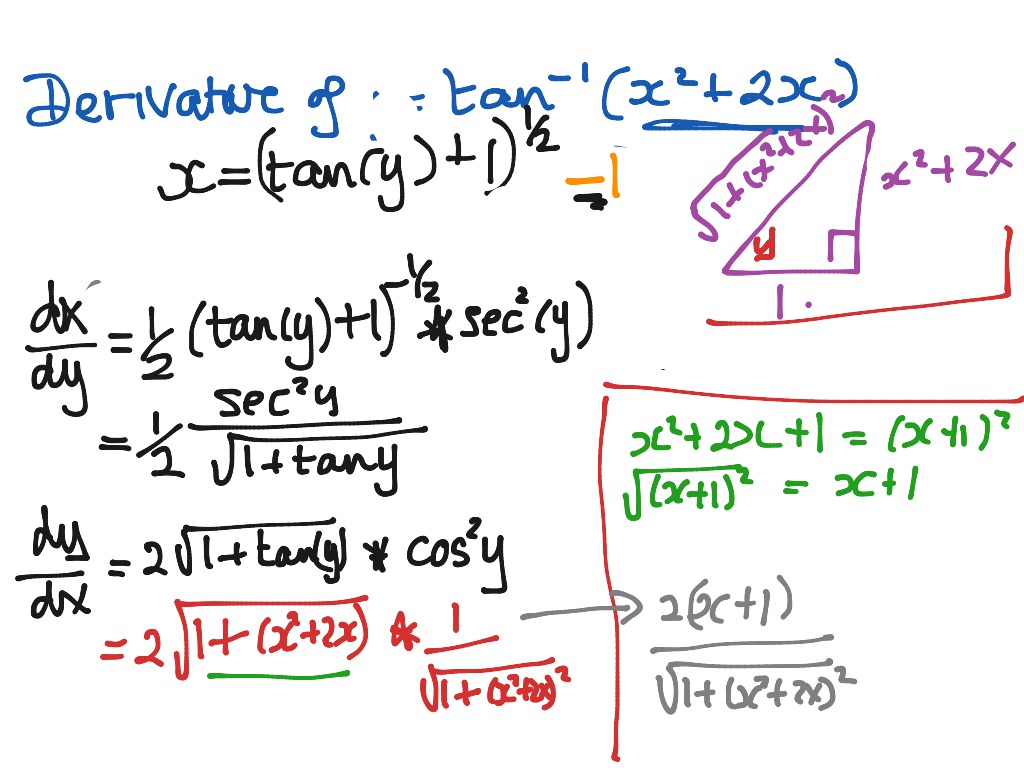
Where
Then
- tan y=x
Using implicit differentiation and solving for dy/dx:
Left side
Right side
Therefore,
Derivative Of Arctan(1/x)
Substituting x=tany in from above, we get
Slope Of Tangent Line Derivative
Tangent Lines
The first problem that we’re going to take a look at is the tangent line problem. Before getting into this problem it would probably be best to define a tangent line.
A tangent line to the function f(x) at the point x=a is a line that just touches the graph of the function at the point in question and is “parallel” (in some way) to the graph at that point. Take a look at the graph below.
In this graph, the line is a tangent line at the indicated point because it just touches the graph at that point and is also “parallel” to the graph at that point. Likewise, at the second point shown, the line does just touch the graph at that point, but it is not “parallel” to the graph at that point and so it’s not a tangent line to the graph at that point.
At the second point shown (the point where the line isn’t a tangent line), we will sometimes call the line a secant line.
We’ve used the word parallel a couple of times now and we should probably be a little careful with it. In general, we will think of a line and a graph as being parallel at a point if they are both moving in the same direction at that point. So, in the first point above the graph and the line are moving in the same direction and so we will say they are parallel at that point. At the second point, on the other hand, the line and the graph are not moving in the same direction so they aren’t parallel at that point.
Okay, now that we’ve gotten the definition of a tangent line out of the way let’s move on to the tangent line problem.
What Are The Derivative Of Tangent?
Derivatives Of Trigonometric Functions. The Basic Trigonometric Functions Include The Following 6 Functions: Sine (Sinx), Cosine (Cosx), Tangent (Tanx), Cotangent (Cotx), Secant (Secx) And Cosecant (Cscx). All These Functions Are Continuous And Differentiable In Their Domains.
What Is Derivative Of Tangent, An Inverse Tangent?
The Arctangent Of X Is Defined As The Inverse Tangent Function Of X When X Is Real (X∈ℝ). When The Tangent Of Y Is Equal To X: Tan Y = X. Then The Arctangent Of X Is Equal To The Inverse Tangent Function Of X, Which Is Equal To Y: Arctan X= Tan-1 X = Y.
What Is The Derivative Of Sin2X?
Namely, Dy/Dx= 2*Cos(2X). Remember That The Chain Rule States That One “Differentiates The Outside, Leaving The Inside Alone, Then Differentiates The Inside Function.” The Derivative Of The Sin(X) With Respect To X Is The Cos(X), And The Derivative Of 2X With Respect To X Is Simply 2.
What Is a Derivative Of Cos 2X?
Derivative Of Arctan
The Derivative Of Cos(2X) Is -2Sin(2X). The Process Of Finding This Derivative Uses The Chain Rule. We Can Use Integrals To Check Our Work When Finding Derivatives. If D(X) Is The Derivative Of F(X), Then The Integral Of D(X) Is F(X) + C, Where C Is A Constant.
What Is Formula Of Sin2X?
Double-angle Formulas: Sin 2X = 2Sin X Cos X, Cos 2X = Cos2X − Sin2X = 2Cos2X − 1=1 − 2Sin2X.
The inverse hyperbolic tangent (Zwillinger 1995, p. 481; Beyer 1987, p. 181), sometimes called the area hyperbolic tangent (Harris and Stocker 1998, p. 267), is the multivalued function that is the inverse function of the hyperbolic tangent.
The function is sometimes denoted (Jeffrey 2000, p. 124) or (Gradshteyn and Ryzhik 2000, p. xxx). The variants or (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values of the inverse hyperbolic tangent, although this distinction is not always made. Worse yet, the notation is sometimes used for the principal value, with being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). Note that in the notation , is the hyperbolic tangent and the superscript denotes an inverse function, not the multiplicative inverse.
The principal value of is implemented in the Wolfram Language as ArcTanh[z] and in the GNU C library as atanh(double x).
The inverse hyperbolic tangent is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segments and . This follows from the definition of as
Derivative Of Arctanh
The inverse hyperbolic tangent is given in terms of the inversetangent by
(Gradshteyn and Ryzhik 2000, p. xxx). For real , this simplifies to
The derivative of the inverse hyperbolic tangent is
and the indefinite integral is
It has special values
(6) |
(8) |
It has Maclaurin series
(10) |
(12) |
(OEIS A005408).
An indefinite integral involving is given by
(14) |
(16) |
when .
SEE ALSO:Hyperbolic Tangent, Inverse Hyperbolic Cotangent, Inverse Hyperbolic FunctionsRELATED WOLFRAM SITES:https://functions.wolfram.com/ElementaryFunctions/ArcTanh/
REFERENCES:Abramowitz, M. and Stegun, I. A. (Eds.). 'Inverse Hyperbolic Functions.' §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
GNU C Library. 'Mathematics: Inverse Trigonometric Functions.' https://www.gnu.org/manual/glibc-2.2.3/html_chapter/libc_19.html#SEC391.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. xxx, 2000.
Harris, J. W. and Stocker, H. Handbookof Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Jeffrey, A. 'Inverse Trigonometric and Hyperbolic Functions.' §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 124-128, 2000.
Sloane, N. J. A. Sequence A005408/M2400in 'The On-Line Encyclopedia of Integer Sequences.'
Spanier, J. and Oldham, K. B. 'Inverse Trigonometric Functions.' Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Zwillinger, D. (Ed.). 'Inverse Hyperbolic Functions.' §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.
Referenced on Wolfram|Alpha: Inverse Hyperbolic TangentCITE THIS AS:Weisstein, Eric W. 'Inverse Hyperbolic Tangent.'From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/InverseHyperbolicTangent.html